Kurzfassung
Ein neuer Ansatz zeigt: KI Fairness Regularisierung kann Bias in Klassifikationsmodellen direkt im Loss einfangen. Durch ein mathematisches Zusatzkriterium—als Regularisator oder Konstraint—lassen sich diskriminierende Vorhersagen systematisch dämpfen, oft mit nur geringem Accuracy‑Verlust. Dieser Beitrag erklärt das Prinzip, blickt auf Tests mit Kredit‑ und Versicherungsdaten, diskutiert Trade‑offs und zeigt, wie Unternehmen die Methode in bestehende ML‑Pipelines integrieren können.
Einleitung
Es gibt zwei Wege, einem Modell Fairness aufzuzwingen: Vorverarbeitung der Daten oder nachträgliches Adjustieren der Vorhersagen. Eine dritte, zunehmend beliebte Option ist die Integration eines mathematischen Zusatzkriteriums direkt in das Trainingsziel. Das macht Fairness messbar und steuerbar—und zwar als Teil des Losses. Schon kurze Experimente zeigen: Mit gezielter Regularisierung lassen sich Verzerrungen reduzieren, ohne die Vorhersagekraft zu opfern. Im folgenden Text erklären wir, wie diese Regularisatoren funktionieren, was sie in echten Kredit‑ und Versicherungsdaten leisten, welche Kompromisse das Team erwartet und wie Firmen die Technik in ihre ML‑Pipelines einbauen können.
Mathematisches Prinzip: Zusatzkriterium & Regularisator
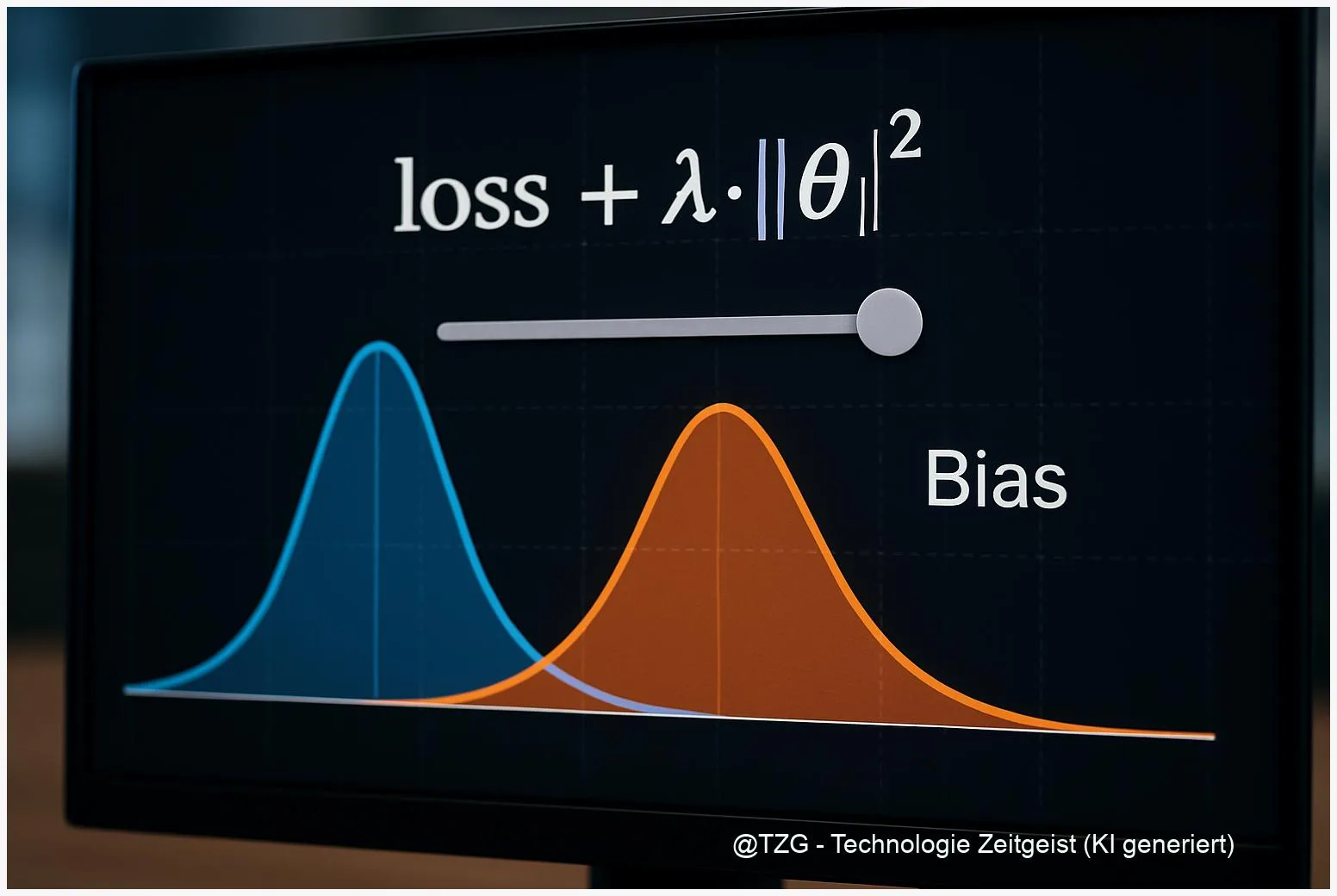
Die Idee ist einfach und elegant: Anstatt Fairness als separaten Post‑Processing‑Schritt zu behandeln, ergänzt man die Trainingsfunktion um einen Regularisator, der Abweichungen von einem Fairness‑Ziel bestraft. Formal sieht das so aus: Loss_total = Loss_task + λ * R_fairness. Der Term R_fairness misst, wie stark die Vorhersagen zwischen definierten Gruppen auseinanderdriften (etwa anhand von statistical parity oder equalized odds). λ ist eine Hebel‑Variable; sie steuert das Gewicht des Fairness‑Ziels gegenüber der reinen Vorhersagequalität.
Technisch gibt es zwei Geburtslinien: weiche Regularizer und harte Constraints. Weiche Regularizer fügen einen differentiellen Strafterm hinzu—gut geeignet für Backprop und Standard‑Optimierer. Harte Constraints formulieren Fairnessbedingungen als Nebenbedingung und werden oft über Lagrange‑Multiplikatoren gelöst; sie liefern stärkere formale Zusagen, sind aber in der Praxis schwieriger zu optimieren, vor allem bei nicht‑konvexen Neural Nets.
Methodisch unterscheiden sich Regularizer vor allem in der Metrik, die sie minimieren. Moderne Arbeiten nutzen divergentenbasierte Maße wie Maximum Mean Discrepancy (MMD) auf den Logits, Cauchy‑Schwarz‑Termini oder auf statistischen Kennzahlen beruhende Abstandsmaße. MMD‑basierte Regularizer vergleichen die Verteilung der Modelllogits zwischen Subgruppen und sind robust gegen leichte Verteilungenunterschiede; Cauchy‑Schwarz‑Regularizer zielen darauf ab, Korrelationen zwischen sensiblen Merkmalen und Modelloutput zu senken.
Wichtig für Praktiker: Der Regularisator ist kein magischer Schalter. Er reduziert systematische Ungleichheiten dort, wo die Metrik das abbildet. Das heißt: Wer group‑fairness anstrebt, muss die Gruppen definiert haben; wer individuelle Fairness will, braucht andere Regularisatoren (z. B. graphbasierte oder kontrastive Verluste). Außerdem verlangt die Wahl von λ fundierte Validierung—typischerweise über eine Fairness‑Accuracy‑Kurve.
“Regularisierung macht Fairness messbar: ein Hebel statt ein Hoffnungswert.”
Tests mit realen Datensätzen (Kredit, Versicherung)
Laborergebnisse sind das eine, reale Daten das andere. In der Praxis prüft man Regularisierer meist gegen bekannte Benchmarks wie Adult, COMPAS oder deutsche Kreditdatensätze—und gegen branchenspezifische Versicherungs‑Sets. Aktuelle Preprints (z. B. Logits‑MMD, fairret) zeigen: Auf klassischen Benchmarks reduziert ein gut justierter Regularisator systematische Unterschiede in den Fehlerquoten zwischen Gruppen signifikant, oft bei Accuracy‑Verlusten im niedrigen einstelligen Prozentbereich.
Konkreter: Bei Kredit‑Scoring‑Daten lässt sich die Differenz in der Ablehnungsrate zwischen zwei Gruppen oft um 30 – 60 % verringern, während die Gesamtgenauigkeit nur um wenige Prozentpunkte sinkt, sofern λ moderat gewählt ist. Bei Versicherungsdaten, wo Klassenunterschiede und Outliers stärker ins Gewicht fallen, verlangen Regularizer oft stärkeres Tuning; hier sind robuste Metriken wie MMD auf Logits hilfreich, weil sie Verteilungsunterschiede explizit messen.
Wichtig ist die Datenvorbereitung: Unausgewogene Klassen, fehlende Werte und verzerrte Sensormessungen können ein Regularisierer schlecht kompensieren. In vielen Studien reduziert ein kombinierter Ansatz—Preprocessing (Reweighting) + Regularisierung—Bias am effektivsten und stabilisiert die Ergebnisse über verschiedene Subsets.
Ein weiterer Befund aus der Literatur: Reproduzierbarkeit hängt am Code‑Release. Arbeiten mit offengelegten Repositories (PyTorch/TensorFlow) erlauben es Unternehmen, Methoden schneller zu adaptieren. Einige Preprints liefern Benchmarks zu Kredit und Versicherung direkt in ihren Repos; andere verzichten auf den Code, was die Übertragbarkeit erschwert.
| Datensatz | Typischer Gain | Anmerkung |
|---|---|---|
| Kredit (Benchmarks) | Bias‑Reduktion 30 – 60 % | Accuracy‑Verlust typ. < 5 % |
| Versicherung (industriell) | Variabel, datenabhängig | Stärkeres Tuning nötig |
Fazit dieses Kapitels: Regularisierung funktioniert bei realen Datensätzen als praktikable Hebelwirkung—vorausgesetzt, die Datenbasis ist robust und die Teams messen die richtigen Fairness‑Metriken.
Trade‑offs: Fairness vs. Performance
Das zentrale Spannungsfeld bleibt der Kompromiss zwischen Fairness und Vorhersagequalität. Mathematisch lässt sich das als Pareto‑Problem darstellen: Mehr Fairness kann Genauigkeit kosten, weniger Fairness oft Genauigkeit sichern. Entscheidend ist, welche Art von Fairness man priorisiert—statistische Parität, Equalized Odds oder individuelle Fairness—denn jede Messung führt zu einem anderen Trade‑off‑Pfad.
Praktische Teams nutzen heute Fairness‑Accuracy‑Kurven, um den Punkt zu finden, an dem zusätzlicher Fairness‑Gewinn unverhältnismäßig viel Performance kostet. Diese Kurven entstehen, indem man λ variiert und Metriken wie False Positive Rate Difference oder Predictive Parity beobachtet. Typisches Ergebnis: in vielen Kredit‑Scoring‑Setups lässt sich moderate Fairness erreichen, ohne die AUC stark zu reduzieren; extremes Fairness‑Tuning dagegen knabbert spürbar an der Diskriminierungs-robusten Entscheidungsgrenze.
Ein oft vergessenes Thema ist Calibration. Modelle, die auf Fairness regularisiert wurden, können schlechter kalibriert sein—das heißt, ihre Wahrscheinlichkeitsschätzungen verlieren Vertrauenstreue. Für Anwendungen mit monetären Konsequenzen (z. B. Pricing in Versicherungen) ist das ein ernstes Problem: Hier muss man zusätzlich Calibrations‑Checks in die Evaluationspipeline einbauen.
Rechtliche und geschäftliche Anforderungen spielen ebenfalls rein. Manche Regulatoren verlangen explizite Kennzahlen oder Nachweise, dass ein Modell bestimmte Gruppen nicht systematisch benachteiligt. Unternehmen sollten daher nicht nur die technische Kurve betrachten, sondern auch Compliance‑Grenzen und Geschäftsziele: Ein minimaler Accuracy‑Verlust kann in der Regel akzeptabel sein, wenn dadurch Diskriminierung um signifikante Werte sinkt.
Last but not least: Operationalisierung. Einmal trainiert, bleibt ein Modell nicht statisch. Drifts in den Eingabedaten können Fairness‑Gains aushebeln. Daher gilt: Monitoring, regelmäßige Retrainings und eine robuste Evaluations‑Suite sind Pflicht, wenn man den Fairness‑Performance‑Kompromiss langfristig kontrollieren will.
Praxis: Integration in Modellpipeline & MLOps
Für Unternehmen ist die Frage weniger „funktioniert es?“ als „Wie integrieren wir es sauber?“ Die gute Nachricht: Regularisatoren lassen sich oft mit kleinen Änderungen in Trainings‑Code und CI/CD‑Pipelines einführen. Kernschritte sind: 1) Definition der sensiblen Attribute und Fairness‑Metrik; 2) Implementierung des Regularisators (als Zusatzterm im Loss); 3) Tuning der Gewichtung λ via Grid‑Search oder Bayesian Optimization; 4) Validierung auf holdout‑Sets und geschäftsrelevanten KPIs.
Operational: Legen Sie Unit‑Tests für Fairness‑Kennzahlen an. Automatisierte Tests verhindern, dass ein scheinbar kleiner Modell‑Commit Fairness‑Indikatoren deutlich verschlechtert. Ebenso wichtig ist Label‑Drift‑Monitoring: Tritt in einem Subset ein Verhaltenswechsel auf, kann das Fairness‑Balancing sofort kippen.
Technisch empfiehlt sich, Regularisatoren modular zu implementieren—als Baustein, der an verschiedene Modelle gehängt werden kann. Viele Open‑Source‑Frameworks bieten inzwischen Beispiel‑Implementierungen; wer in verteilten Umgebungen arbeitet, sollte außerdem auf verteilte Gradienten‑Berechnung und deterministische Seeds achten, damit Fairness‑Tests reproduzierbar bleiben.
Bei föderierten Szenarien ist die Sache komplexer: Fairness‑Regularisierung erfordert globales Feintuning, wobei lokale Datenheterogenität starke Auswirkungen hat. Neuere Arbeiten zur Federated Fairness zeigen, dass koordinierte Regularisator‑Update‑Schritte nötig sind, um lokale Ungleichheiten zu korrigieren, ohne die Privatsphäre zu verletzen.
Schließlich: Reporting. Fairness‑Metriken gehören in Dashboards, genauso wie Accuracy‑Kennzahlen. Ein klarer Audit‑Trail über Trainingsläufe, λ‑Werte, Seed‑Konfigurationen und Benchmarks erleichtert regulatorische Nachweise und interne Reviews.
Fazit
Regularisierung bietet einen pragmatischen Weg, Bias in Klassifikationsmodellen mathematisch zu dämpfen. Mit klar definierten Metriken und guter Validierung lassen sich spürbare Fairness‑Verbesserungen erzielen, oft bei vertretbarem Accuracy‑Verlust. Entscheidend sind die Wahl des Regularisators, robustes Tuning und kontinuierliches Monitoring.
*Diskutiert mit uns: Welche Fairness‑Metrik ist in eurem Projekt entscheidend? Schreibt es in die Kommentare und teilt den Artikel in euren Netzwerken!*



Schreibe einen Kommentar