Kernel PCA ist eine Methode zur nichtlinearen Dimensionsreduktion, die mit Hilfe einer Kernel‑Funktion komplexe Muster sichtbar macht. In einfachen Worten nutzt Kernel PCA Ähnlichkeiten zwischen Punkten, um sie in einer neuen Projektion so anzuordnen, dass verborgene Strukturen wie verschlungene Kurven oder gekrümmte Cluster gerade erscheinen. Diese Technik eignet sich besonders für kleine bis mittelgroße Datensätze und ist ein nützliches Werkzeug, wenn lineare Verfahren wie klassische PCA versagen.
Einleitung
Viele einfache Werkzeuge zur Datenanalyse setzen darauf, Daten in geraden Linien oder Ebenen zu ordnen. Wenn Messpunkte aber wie eine gedrehte Spirale oder zwei halbmondförmige Hälften verteilt sind, hilft lineare Analyse wenig. Genau in solchen Fällen kommt Kernel PCA ins Spiel: Es ordnet Daten so, dass nichtlineare Beziehungen in einer niedrigerdimensionalen Darstellung erkennbar werden. Das betrifft nicht nur akademische Übungsdatensätze, sondern auch Bilder, Sensordaten oder Messreihen, bei denen Trends nicht additiv sind.
Im Alltag fällt das auf, wenn einfache Visualisierungen keine sinnvolle Trennung von Gruppen zeigen, obwohl verdeckte Muster vorhanden sind. Kernel PCA nutzt dazu eine mathematische Technik, die oft „Kernel‑Trick” genannt wird: Statt Punkte explizit in einen sehr hohen Merkmalsraum zu rechnen, genügt eine Matrix mit paarweisen Ähnlichkeiten. Für Leserinnen und Leser bedeutet das: komplexe Strukturen können sichtbar werden, ohne dass ein Computer alle neuen Merkmale einzeln berechnen muss.
Was ist Kernel PCA?
Kernel PCA ist eine nichtlineare Verallgemeinerung der klassischen Hauptkomponentenanalyse (PCA). Bei PCA sucht man Richtungen, in denen die Daten am stärksten variieren, und reduziert dadurch die Dimension. Kernel PCA übernimmt diese Idee, führt sie aber in einem impliziten, höherdimensionalen Raum aus, der durch eine Kernel‑Funktion beschrieben wird. Eine Kernel‑Funktion misst die Ähnlichkeit zwischen zwei Punkten, zum Beispiel mit dem weit verbreiteten RBF‑Kernel (auch Gaussian‑Kernel genannt): k(x,y)=exp(−γ||x−y||²). Der Parameter γ steuert, wie lokal oder global Ähnlichkeiten bewertet werden.
Kernel PCA arbeitet nicht mit den ursprünglichen Koordinaten, sondern mit einer n×n‑Matrix der paarweisen Ähnlichkeiten.
Der praktische Ablauf ist überschaubar: 1) Aus den Daten wird die Kernelmatrix K erstellt, 2) K wird zentriert und 3) es wird eine Eigenwertzerlegung durchgeführt. Die führenden Eigenvektoren entsprechen den neuen Hauptkomponenten im impliziten Raum. Wichtig ist: Diese Schritte zeigen, welche Muster wichtig sind, ohne dass man die neue, oft sehr hohe Dimension explizit konstruiert.
Ein zentraler mathematischer Punkt ist die Skalierung. Die Kernelmatrix ist n×n groß (n = Anzahl der Beispiele). Daraus folgen Speicher‑ und Rechenbegrenzungen: Für sehr große Datenmengen wird Kernel PCA schnell teuer. Schölkopf, Smola und Müller stellten dieses Verfahren 1998 vor; diese Studie stammt aus dem Jahr 1998 und ist damit älter als zwei Jahre, bleibt aber die grundlegende Referenz für das Verfahren.
Wenn Zahlen helfen, lässt sich sagen: Speicherbedarf wächst ungefähr quadratisch mit der Anzahl der Punkte, die vollständige Eigenzerlegung kann im praktischen Aufwand kubisch skalieren. Deshalb kommt Kernel PCA vor allem bei Datensätzen bis einige Tausend Beispiele direkt zum Einsatz; für größere Daten sind Approximationen nötig.
Wenn eine Rückprojektion in den ursprünglichen Merkmalsraum nötig ist (sogenannte Pre‑Image‑Problematik), gibt es keine allgemeingültige exakte Lösung. Für typische Anwendungen existieren Näherungsverfahren, die oft ausreichend sind, aber die Einschränkung sollte man kennen.
| Merkmal | Beschreibung | Wert |
|---|---|---|
| Kernel | Funktion zur Messung von Ähnlichkeit | RBF (Standard) |
| Komplexität | Speicher/ Zeit | O(n²) / bis O(n³) |
Kernel PCA im Alltag: ein konkretes Beispiel
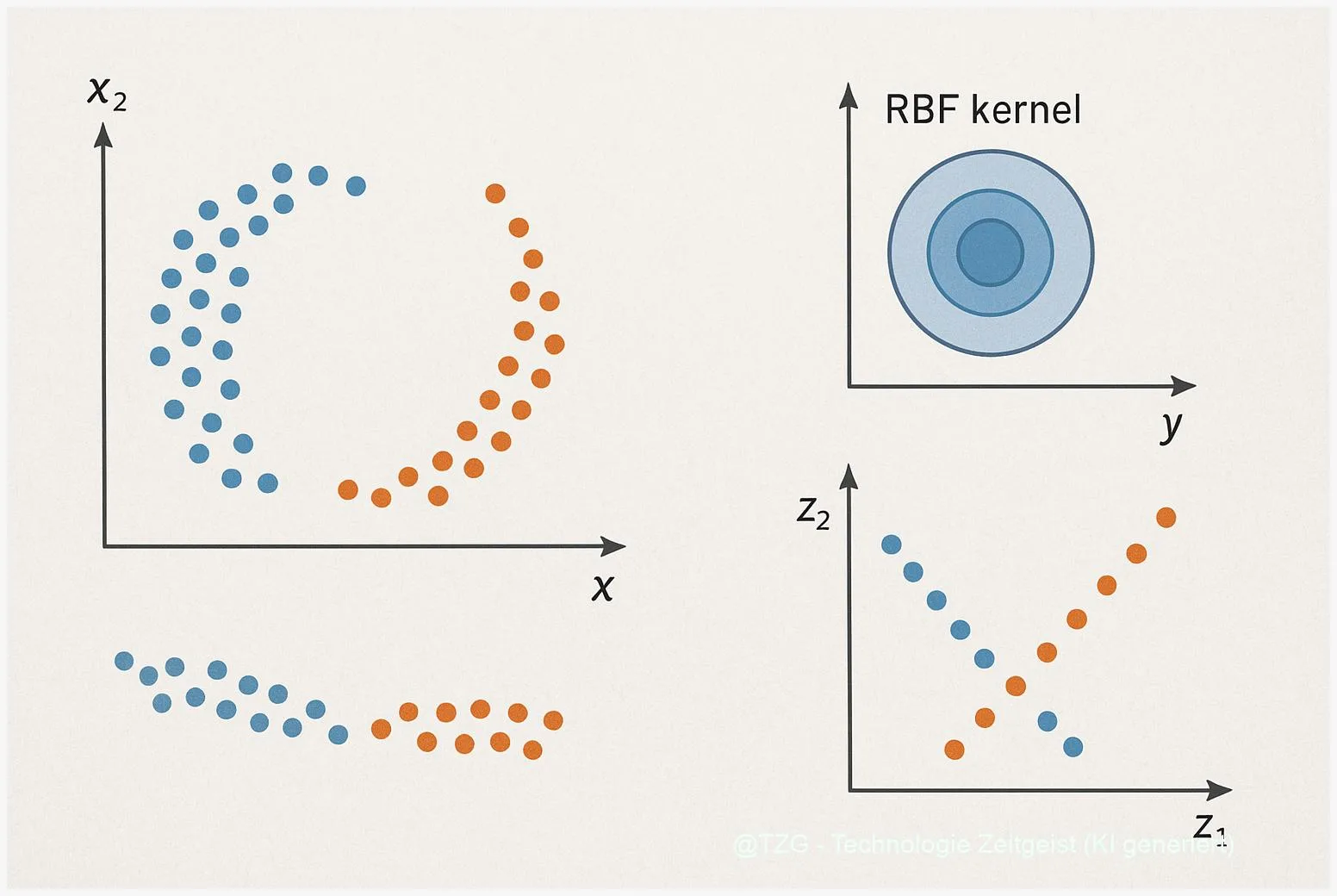
Ein verbreitetes Demonstrationsbeispiel heißt „Two‑Moons”. Dabei liegen Punkte in zwei halbmondförmigen Hälften vor, die sich wie zwei gebogene Halbkreise gegenüberstehen. In der ursprünglichen 2‑D‑Ansicht lassen sich die Gruppen nicht linear trennen. Eine lineare PCA bringt ebenfalls keine Trennung, weil die Varianz in flachen Richtungen liegt.
Setzt man hingegen Kernel PCA mit einem RBF‑Kernel ein, verändern sich die Abstände so, dass die beiden Halbmonde im neuen Raum auseinandergezogen werden. In der Projektion auf die ersten beiden Kernel‑Hauptkomponenten erscheinen die Punkte dann getrennt — ein klassischer visueller Effekt: Die nichtlineare Form wird so „entfaltet”, dass eine lineare Trennung möglich wird. Das ist kein Zauber, sondern das Ergebnis, dass der RBF‑Kernel lokale Nachbarschaften stärker gewichtet als entfernte Paare.
In der Praxis läuft ein einfacher Workflow so: Daten standardisieren, RBF‑Kernel wählen, einen Bereich für γ mit Kreuzvalidierung testen (zum Beispiel ein logarithmisches Raster zwischen 10^−3 und 10^2), die Kernelmatrix berechnen und danach die führenden Komponenten betrachten. Für viele Lehrbeispiele und kleinere Projekte liefert scikit‑learn sofort reproduzierbare Ergebnisse, inklusive Illustrationen des Two‑Moons‑Effekts.
Konkrete Anwendungen reichen von Merkmalsextraktion bei Bildern über Sensordaten bis zu Anomalieerkennung, wenn Abweichungen nicht additiv sind. In der Bildbearbeitung kann Kernel PCA etwa Muster hervorheben, die lineare Methoden übersehen, bei Sensoren hilft es, nichtlineare Drift oder Zusammenhänge zu erkennen.
Ein praktischer Tipp: Visualisieren Sie zuerst klassische PCA und dann Kernel PCA. Gerade bei Laien zeigt das anschaulich den Unterschied und macht transparent, warum die nichtlineare Methode sinnvoll war.
Stärken, Grenzen und Risiken
Kernel PCA punktet durch die Fähigkeit, nichtlineare Strukturen sichtbar zu machen, ohne explizite, hohe Merkmalsräume zu konstruieren. Das ist elegant und in vielen Fällen deutlich leistungsfähiger als lineare PCA. Gleichzeitig ist die Methode anfällig für praktische Schwierigkeiten: Die Wahl der Kernel‑Funktion und ihrer Hyperparameter, vor allem des γ beim RBF‑Kernel, hat großen Einfluss auf das Ergebnis. Es gibt keine universelle Regel für γ; oft sind Kreuzvalidierung oder heuristische Raster nötig.
Ein weiteres Risiko ist die Skalierbarkeit. Bei sehr großen Datensätzen wird die Kernelmatrix zum Flaschenhals. Hier helfen Approximationen wie Nyström‑Methoden oder Random Fourier Features, die die Kernelmatrix näherungsweise darstellen und so Speicher und Rechenzeit reduzieren. Alternativen für Visualisierungen sind auch t‑SNE oder UMAP, die für große Datensätze oft schneller und robustere Visualisierungen liefern.
Die Pre‑Image‑Problematik ist eine methodische Begrenzung: Kernel PCA liefert die Projektion, aber nicht immer eine eindeutige, exakte Rückprojektion in den ursprünglichen Eingaberaum. Für Anwendungen, die eine genaue Rekonstruktion brauchen (etwa feines Bild‑Denoising), ist das relevant. Es existieren Näherungsverfahren, doch die Qualität hängt stark von Regularisierung und Parametereinstellung ab.
Schließlich ist Interpretierbarkeit ein Thema. Die neuen Komponenten sind lineare Kombinationen von Kernelauswertungen und lassen sich nicht so intuitiv deuten wie lineare Achsen. In manchen Anwendungen ist das akzeptabel — in anderen, etwa in sicherheitskritischen Kontexten, verlangt man eher nachvollziehbare Merkmale.
Wohin die Entwicklung gehen kann
Die Forschung und Praxis im Bereich nichtlinearer Dimensionsreduktion entwickelt sich in zwei Richtungen: bessere Skalierbarkeit und bessere Interpretierbarkeit. Für Skalierbarkeit setzen viele Lösungen heute auf Approximationen des Kernels oder auf zufallsbasierte Techniken, die ähnliche Effekte mit deutlich geringerem Rechenaufwand erreichen. Für sehr große Datensätze sind hybride Verfahren denkbar, die Kernel‑Ideen lokal anwenden und Ergebnisse anschließend zusammenführen.
Im Bereich Interpretierbarkeit arbeiten Forscherinnen und Forscher an Methoden, die Kernel‑Komponenten besser erklärbar machen oder die Pre‑Image‑Schätzung zuverlässiger machen. Ebenso gewinnt die Kombination mit neuronalen Netzen an Bedeutung: Deep Kernels koppeln die Flexibilität tiefer Modelle mit den guten Eigenschaften von Kernmethoden.
Für Anwenderinnen und Anwender bedeutet das: Die klassische Kernel PCA bleibt ein solides Werkzeug für kleine bis mittelgroße Probleme und Lehrzwecke. Wenn allerdings große Datenmengen oder strenge Rekonstruktionsanforderungen vorliegen, lohnt sich ein Blick auf moderne Alternativen oder hybride Ansätze. In den kommenden Jahren ist zu erwarten, dass Skalierbarkeits‑Tricks und bessere Pre‑Image‑Techniken Kernel‑Methoden weiter ins praktische Arsenal bringen.
Fazit
Kernel PCA ist ein klares Werkzeug in der Toolbox für nichtlineare Datenanalyse: Es macht verborgene Strukturen sichtbar, indem es Ähnlichkeiten zwischen Punkten nutzt statt auf lineare Achsen zu vertrauen. Die Methode ist besonders nützlich bei kleineren bis mittleren Datensätzen oder als Demonstrationswerkzeug, etwa am Two‑Moons‑Beispiel. Grenzen sind vor allem Rechen‑ und Speicherbedarf sowie die Schwierigkeit einer exakten Rückprojektion. Wer Kernel PCA einsetzt, sollte Parameter sorgfältig wählen und die Ergebnisse stets mit alternativen Methoden vergleichen. So bleibt die Analyse belastbar und nachvollziehbar.

Schreibe einen Kommentar